Helicopter Flight Model Config (XML): Difference between revisions
(syntaxhighlighting + xml fixes) |
m (Improved formatting) |
||
| Line 1: | Line 1: | ||
== Disclaimer == | |||
'''This documentation was reproduced from the official RotorLib Programmer's Guide with permission from [http://www.rtdynamics.com RTDynamics].''' | |||
== What is RotorLib FDM == | |||
Please note that this version of the documentation (3.2) is based on a slightly older version of the library than the one used in TKOH (3.3). As soon as updated official documentation becomes available, we'll update this resource. | |||
== What is RotorLib FDM? == | |||
RotorLib FDM is RTDynamics' rotary wing aircraft flight dynamics model solution. It includes aerodynamic models, ground contact model, flight instrument models and flight control system simulation. | RotorLib FDM is RTDynamics' rotary wing aircraft flight dynamics model solution. It includes aerodynamic models, ground contact model, flight instrument models and flight control system simulation. | ||
RotorLib FDM is designed for pilot-in-the-loop applications such as flight training simulators, mission rehearsal systems and combat training simulators. | RotorLib FDM is designed for pilot-in-the-loop applications such as flight training simulators, mission rehearsal systems and combat training simulators. | ||
== RotorLib Flight Dynamics Model == | == RotorLib Flight Dynamics Model == | ||
=== GenHeli500 model === | === GenHeli500 model === | ||
The generic RotorLib FDM helicopter flight dynamics model is implemented in ''RotorLibFDM::GenHeli500'' class. This class uses several mathematical models as components to create a generic helicopter model. GenHeli500 consists of: | The generic RotorLib FDM helicopter flight dynamics model is implemented in ''RotorLibFDM::GenHeli500'' class. This class uses several mathematical models as components to create a generic helicopter model. GenHeli500 consists of: | ||
* one main rotor and one tail rotor (both based on ''FGRotorMomentumTheory'' model) | * one main rotor and one tail rotor (both based on ''FGRotorMomentumTheory'' model) | ||
* vertical and horizontal stabilizers ( based on ''FGHelicopterStabilizerWing'' ) | * vertical and horizontal stabilizers ( based on ''FGHelicopterStabilizerWing'' ) | ||
* fuselage model ( ''FGHeliFuselage100'' ) | * fuselage model ( ''FGHeliFuselage100'' ) | ||
* a user defined number of ground contacts which can be configured as steerable or non-steerable gears and body contacts . | * a user defined number of ground contacts which can be configured as steerable or non-steerable gears and body contacts . | ||
* extensible engine model | * extensible engine model | ||
* drive train model | * drive train model | ||
* extensible flight control system | * extensible flight control system | ||
* flight instruments | * flight instruments | ||
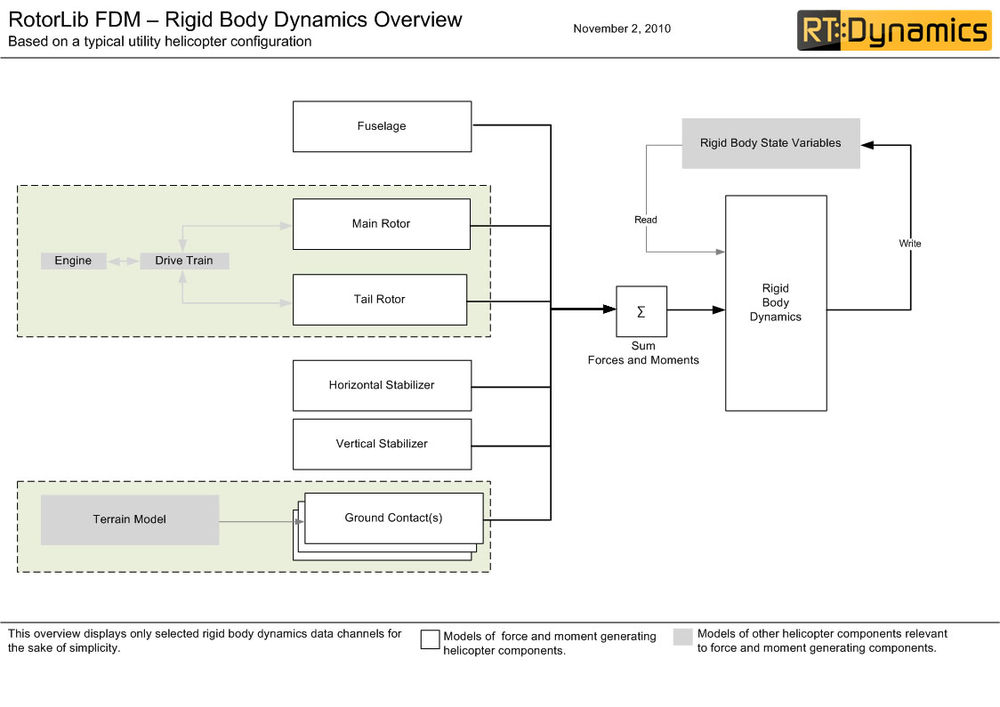
Forces and moments computed by models above are used by a real-time rigid body dynamics model to update the rigid body state of the helicopter. Below you can find an overview of the rigid body dynamics used in RotorLib. | Forces and moments computed by models above are used by a real-time rigid body dynamics model to update the rigid body state of the helicopter. Below you can find an overview of the rigid body dynamics used in RotorLib. | ||
[[Image:RLIBDOC01.jpg]] | [[Image:RLIBDOC01.jpg|thumb|1000px|center]] | ||
=== GenHeli500 configuration === | === GenHeli500 configuration === | ||
| Line 94: | Line 97: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
* '''MomentsOfInertia''' Moments of inertia of the helicopter body are defined here. Available parameters are Ixx, Iyy, Izz and Iyz (in Kg*m^2) | * '''MomentsOfInertia''' - Moments of inertia of the helicopter body are defined here. Available parameters are Ixx, Iyy, Izz and Iyz (in Kg*m^2) | ||
* '''Mass''' mass parameter defines the mass of the helicopter in Kg. | * '''Mass''' - mass parameter defines the mass of the helicopter in Kg. | ||
* '''Fuselage''' GenHeli500 fuselage model is implemented using RotorLibFDM::FGHeliFuselage100 model. See Fuselage section below for details. | * '''Fuselage''' - GenHeli500 fuselage model is implemented using RotorLibFDM::FGHeliFuselage100 model. See Fuselage section below for details. | ||
* '''Engines''' In this section, engines are configured. Configuration for the chosen engine model must be provided inside the <Engine> </Engine> tags. | * '''Engines''' - In this section, engines are configured. Configuration for the chosen engine model must be provided inside the <Engine> </Engine> tags. | ||
* '''ControlSystem''' Automatic flight control system configuration. In this section a multitude of flight control system components can be defined. Each component should be defined in a separate <FCSComponent> section. type parameter in FCSComponent defines which component type (e.g. FCSRotationDamper ) will be created. Inside the <FCSComponent> </FCSComponent> configuration parameters of the chosen component model has to be provided. | * '''ControlSystem''' - Automatic flight control system configuration. In this section a multitude of flight control system components can be defined. Each component should be defined in a separate <FCSComponent> section. type parameter in FCSComponent defines which component type (e.g. FCSRotationDamper ) will be created. Inside the <FCSComponent> </FCSComponent> configuration parameters of the chosen component model has to be provided. | ||
* '''MainRotor and TailRotor''' In these sections main and tail rotors are configured. Rotors use RTD::FGRotorMomentumTheory rotor model. See Rotor model section for details. | * '''MainRotor and TailRotor''' - In these sections main and tail rotors are configured. Rotors use RTD::FGRotorMomentumTheory rotor model. See Rotor model section for details. | ||
* '''HorizontalStabilizerRight , HorizontalStabilizerLeft and VerticalStabilizer''' Stabilizers use RTD::FGHelicopterStabilizerWing wing model. See Stabilizers section for details. | * '''HorizontalStabilizerRight, HorizontalStabilizerLeft and VerticalStabilizer''' - Stabilizers use RTD::FGHelicopterStabilizerWing wing model. See Stabilizers section for details. | ||
* '''GroundContacts''' In this section ground contacts of the helicopter are configured. See Ground Contacts section for details. | * '''GroundContacts''' - In this section ground contacts of the helicopter are configured. See Ground Contacts section for details. | ||
=== Rotor Model === | === Rotor Model === | ||
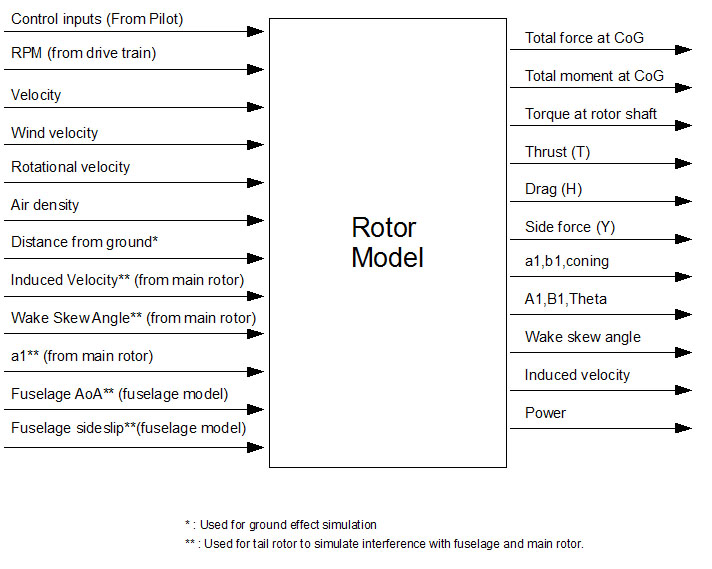
''GenHeli500'' uses ''FGRotorMomentumTheory'' class as rotor model. This class simulates aerodynamic and mechanical behavior of a rotor. It is used for both main and tail rotors. ''FGRotorMomentumTheory'' uses momentum theory and certain blade element theory elements to compute the forces and moments. It also outputs values, such as induced velocity or wake skew angle, that are used as input by other mathematical models, such as fuselage model. Inputs and outputs of the model are summarized below: | ''GenHeli500'' uses ''FGRotorMomentumTheory'' class as rotor model. This class simulates aerodynamic and mechanical behavior of a rotor. It is used for both main and tail rotors. ''FGRotorMomentumTheory'' uses momentum theory and certain blade element theory elements to compute the forces and moments. It also outputs values, such as induced velocity or wake skew angle, that are used as input by other mathematical models, such as fuselage model. Inputs and outputs of the model are summarized below: | ||
[[Image:RLIBDOC02.jpg|thumb|800px|center|Figure 6.1 Rotor model inputs and outputs]] | |||
[[Image:RLIBDOC02.jpg]] | |||
A helicopter rotor produces thrust by setting the air around it in motion. As a result, a rotor operates in the airflow which is induced by itself. Because of the induced airflow, rotor blades operate in a downward air stream which reduces the effective angle of attack which in turn results in reduced lift. In momentum theory of rotors, the law of conservation of momentum is used on the airflow and an equation that relates T (thrust produced by the rotor) to Vi (speed of the air stream at the rotor disc) is obtained. A second equation that relates T and Vi can be written with blade element theory. Resulting equations are not linear and they are not solvable with algebraic methods hence an iterative numerical solution is implemented. | A helicopter rotor produces thrust by setting the air around it in motion. As a result, a rotor operates in the airflow which is induced by itself. Because of the induced airflow, rotor blades operate in a downward air stream which reduces the effective angle of attack which in turn results in reduced lift. In momentum theory of rotors, the law of conservation of momentum is used on the airflow and an equation that relates T (thrust produced by the rotor) to Vi (speed of the air stream at the rotor disc) is obtained. A second equation that relates T and Vi can be written with blade element theory. Resulting equations are not linear and they are not solvable with algebraic methods hence an iterative numerical solution is implemented. | ||
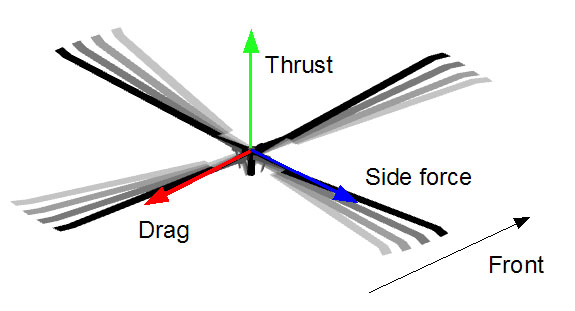
Simulation update of the rotor model begins by solving above equations and finding T (Thrust) and Vi (induced velocity). Once we know T and Vi, H (Drag) and Y(Side force) are computed. | Simulation update of the rotor model begins by solving above equations and finding T (Thrust) and Vi (induced velocity). Once we know T and Vi, H (Drag) and Y(Side force) are computed. | ||
[[Image:RLIBDOC03.jpg]] | [[Image:RLIBDOC03.jpg|thumb|800px|center|Figure 6.2 Main rotor forces]] | ||
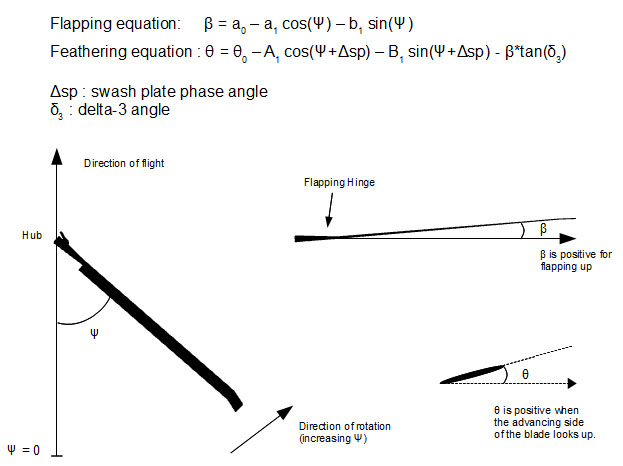
The next step in rotor update is updating flapping dynamics. A fully articulated helicopter rotor has flapping, lead-lag and feathering hinges. These hinges provide a certain amount of independent motion capability to the blades. Blades can lead and lag the rotation of the hub on the disc plane. Moreover, because of the flapping hinge, they can move below or above the disc plane. These extra degrees of freedom have effects on power consumption, forces, moments and handling quality. ''FGRotorMomentumTheory'' simulates first order flapping dynamics: It computes a1,b1and a0 (coning angle). Higher order terms in the flapping equation and the lead-lag motion is ignored since their effect on the rotor is less important compared to the first order flapping terms. See following figure for the details of the flapping equation and geometry. | The next step in rotor update is updating flapping dynamics. A fully articulated helicopter rotor has flapping, lead-lag and feathering hinges. These hinges provide a certain amount of independent motion capability to the blades. Blades can lead and lag the rotation of the hub on the disc plane. Moreover, because of the flapping hinge, they can move below or above the disc plane. These extra degrees of freedom have effects on power consumption, forces, moments and handling quality. ''FGRotorMomentumTheory'' simulates first order flapping dynamics: It computes a1,b1and a0 (coning angle). Higher order terms in the flapping equation and the lead-lag motion is ignored since their effect on the rotor is less important compared to the first order flapping terms. See following figure for the details of the flapping equation and geometry. | ||
[[Image:RLIBDOC04.jpg|thumb|800px|center|Figure 6.3 Flapping geometry and equation]] | |||
[[Image:RLIBDOC04.jpg]] | |||
After flapping dynamics, power is computed. Power is computed as a sum of following components: | After flapping dynamics, power is computed. Power is computed as a sum of following components: | ||
# Induced power : Power consumption due to induced air flow. | |||
# Parasite power : Power consumption due to the drag of fuselage, rotor hub, external stores etc. | |||
# Climbing power : Power consumption/gain due to altitude change (potential energy change). | |||
# Profile power : Power consumption due to blade profile drag. | |||
By computing the power consumption of the rotor we also get information about the torque acting on the rotor shaft ( P = angular speed x torque ). This torque is the load the rotor is putting on the engine through the drive train, hence it is an input to the drive train model. Moreover, it also acts on the helicopter fuselage and tries to rotate it in the opposite direction of rotor and hence has effects on flight handling. | By computing the power consumption of the rotor we also get information about the torque acting on the rotor shaft ( P = angular speed x torque ). This torque is the load the rotor is putting on the engine through the drive train, hence it is an input to the drive train model. Moreover, it also acts on the helicopter fuselage and tries to rotate it in the opposite direction of rotor and hence has effects on flight handling. | ||
| Line 138: | Line 134: | ||
After power, moments at the CoG of the helicopter and rotor wake skew angle are computed. Rotor wake skew angle, along with Vi, is used by other components (fuselage, stabilizers and tail rotor) as input. | After power, moments at the CoG of the helicopter and rotor wake skew angle are computed. Rotor wake skew angle, along with Vi, is used by other components (fuselage, stabilizers and tail rotor) as input. | ||
[[Image:RLIBDOC05.jpg|thumb|800px|center|Figure 6.4 Rotor wake skew angle]] | |||
If the model is used to simulate a tail rotor, interference with main rotor and fuselage is taken into account in all above steps. | |||
==== FGRotorMomentumTheory configuration format ==== | ==== FGRotorMomentumTheory configuration format ==== | ||
| Line 170: | Line 165: | ||
</MainRotor> | </MainRotor> | ||
</syntaxhighlight> | </syntaxhighlight> | ||
===== Geometry ===== | ===== Geometry ===== | ||
This section defines the rotor geometry. All vectors are in RTDynamics coordinate system ( Y forward, X rightward, Z up). They are defined relative to the helicopter body coordinate system. | This section defines the rotor geometry. All vectors are in RTDynamics coordinate system ( Y forward, X rightward, Z up). They are defined relative to the helicopter body coordinate system. | ||
* Position : position of the rotor hub relative to the center of gravity of the helicopter. In meters. | * Position: position of the rotor hub relative to the center of gravity of the helicopter. In meters. | ||
* Tilt : orientation of the rotor. | * Tilt: orientation of the rotor. | ||
** lateralTilt : Lateral tilt of the rotor in degrees. Positive values denote a rightward tilt. | ** lateralTilt: Lateral tilt of the rotor in degrees. Positive values denote a rightward tilt. | ||
** longitudinalTilt : Longitudinal tilt of the rotor in degrees. Positive values denote a backward tilt. This parameter is negative for most of the helicopters. | ** longitudinalTilt: Longitudinal tilt of the rotor in degrees. Positive values denote a backward tilt. This parameter is negative for most of the helicopters. | ||
* Blades : Blade parameters. | * Blades: Blade parameters. | ||
** count : Number of blades. | ** count: Number of blades. | ||
** radius : Radius of the blades in meters. | ** radius: Radius of the blades in meters. | ||
** chord : Chord (width) of the blades in meters. | ** chord: Chord (width) of the blades in meters. | ||
** hingeOffset : Distance of the flapping hinge from rotation center in meters. | ** hingeOffset: Distance of the flapping hinge from rotation center in meters. | ||
===== MechanicalFeatures : Mechanical features of the rotor | ===== MechanicalFeatures: Mechanical features of the rotor ===== | ||
* Ir: Moment of inertia (rotational inertia) of the rotor about the axis of rotation. In kg*m^2. | |||
* Ir : Moment of inertia (rotational inertia) of the rotor about the axis of rotation. In kg*m^2. | * Ib: Moment of inertia (rotational inertia) of a blade about the flapping hinge. In kg*m^2. | ||
* gearRatio: Gear ratio between the engine and the rotor. rotor RPM = engine RPM / gearRatio. | |||
* Ib : Moment of inertia (rotational inertia) of a blade about the flapping hinge. In kg*m^2. | |||
* gearRatio : Gear ratio between the engine and the rotor. rotor RPM = engine RPM / gearRatio. | |||
===== AerodynamicFeatures ===== | ===== AerodynamicFeatures ===== | ||
* Blades | * Blades | ||
** liftCurveSlope : Slope of the blade lift curve. X axis of the curve is assumed to be in degrees. This parameter does not have a unit. Example: If a lift curve has Clmax = 1.5 at 15 degrees , liftCurveSlope will be 1.5/15 = 0.1. | ** liftCurveSlope: Slope of the blade lift curve. X axis of the curve is assumed to be in degrees. This parameter does not have a unit. Example: If a lift curve has Clmax = 1.5 at 15 degrees , liftCurveSlope will be 1.5/15 = 0.1. | ||
** zeroLiftDragCoefficient : Drag coefficient of the blades at zero lift. This parameter does not have a unit. | ** zeroLiftDragCoefficient: Drag coefficient of the blades at zero lift. This parameter does not have a unit. | ||
** twist : Blade twist in degrees. | ** twist: Blade twist in degrees. | ||
* Controls | * Controls | ||
** A1UL : Upper limit of lateral swash plate tilt in degrees. | ** A1UL: Upper limit of lateral swash plate tilt in degrees. | ||
** A1LL : Lower limit of lateral swash plate tilt in degrees. | ** A1LL: Lower limit of lateral swash plate tilt in degrees. | ||
** B1UL : Upper limit of longitudinal swash plate tilt in degrees. | ** B1UL: Upper limit of longitudinal swash plate tilt in degrees. | ||
** B1LL : Lower limit of longitudinal swash plate tilt in degrees. | ** B1LL: Lower limit of longitudinal swash plate tilt in degrees. | ||
** thetaLL : Minimum pitch of the blades due to collective input. When collective input is 0 blade pitch will be thetaLL degrees. | ** thetaLL: Minimum pitch of the blades due to collective input. When collective input is 0 blade pitch will be thetaLL degrees. | ||
** thetaUL : Maximum pitch of the blades due to collective input. When collective input is 1 blade pitch will be thetaUL degrees. | ** thetaUL: Maximum pitch of the blades due to collective input. When collective input is 1 blade pitch will be thetaUL degrees. | ||
* Power | * Power | ||
inducedPowerCorrectionFactor : Due to various reasons, momentum theory requires an empirical correction factor for the computation of the induced power. This parameter is used for this purpose. | inducedPowerCorrectionFactor: Due to various reasons, momentum theory requires an empirical correction factor for the computation of the induced power. This parameter is used for this purpose. | ||
* DesignRPM | * DesignRPM | ||
rpm : Design RPM of the rotor. If no engine is connected to the helicopter, rotor will rotate with this speed. In revolutions per minute. | ** rpm: Design RPM of the rotor. If no engine is connected to the helicopter, rotor will rotate with this speed. In revolutions per minute. | ||
* GroundEffect | * GroundEffect | ||
magnitude : An empirical parameter which defines the magnitude of the ground effect. This parameter does not have a unit. | ** magnitude: An empirical parameter which defines the magnitude of the ground effect. This parameter does not have a unit. | ||
=== Fuselage === | === Fuselage === | ||
Fuselage model is implemented in ''FGHeliFuselage100'' class. Inputs and outputs of the model are summarized in the following diagram: | Fuselage model is implemented in ''FGHeliFuselage100'' class. Inputs and outputs of the model are summarized in the following diagram: | ||
[[Image:RLIBDOC06.jpg|thumb|center|800px|Figure 6.5 FGHeliFuselage100 model inputs and outputs]] | |||
[[Image:RLIBDOC06.jpg]] | |||
All forces and moments are computed at the center of gravity. | All forces and moments are computed at the center of gravity. | ||
| Line 223: | Line 214: | ||
During simulation update, fuselage model initially computes the effective relative wind (in other words, air stream velocity) acting on the fuselage. To compute the effective relative wind helicopter velocity, wind velocity and the main rotor downwash is used. Downwash is characterized by rotor wake skew angle and induced velocity, which are outputs of the rotor model (see Rotor model section for details). Unfortunately, these values can not be used directly to compute the rotor's effect on the fuselage because they are only reference values and the actual induced velocity changes depending on the position on the helicopter. Different parts of the fuselage receive different amount of induced air stream. Therefore there are two curve sets in the configuration file ( ''MainRotorDownwash and MainRotorInplanewash'') which define downwash and inplanewash coefficients depending on the rotor wake skew angle. Using induced velocity output of the main rotor and these curves (as look-up tables indexed by rotor wake angle) final air stream velocity vector is computed. | During simulation update, fuselage model initially computes the effective relative wind (in other words, air stream velocity) acting on the fuselage. To compute the effective relative wind helicopter velocity, wind velocity and the main rotor downwash is used. Downwash is characterized by rotor wake skew angle and induced velocity, which are outputs of the rotor model (see Rotor model section for details). Unfortunately, these values can not be used directly to compute the rotor's effect on the fuselage because they are only reference values and the actual induced velocity changes depending on the position on the helicopter. Different parts of the fuselage receive different amount of induced air stream. Therefore there are two curve sets in the configuration file ( ''MainRotorDownwash and MainRotorInplanewash'') which define downwash and inplanewash coefficients depending on the rotor wake skew angle. Using induced velocity output of the main rotor and these curves (as look-up tables indexed by rotor wake angle) final air stream velocity vector is computed. | ||
[[Image:RLIBDOC07.jpg|thumb|center|800px|Figure 6.6 Velocity of air stream at the fuselage CoP (center of pressure)]] | |||
Both the magnitude and direction of the incoming air stream affect the resulting forces and moments so the angle of attack and side slip angles for the effective relative wind are computed. Configuration parameters of the fuselage includes two curves for each force and moment. One of them bases on angle of attack and the other on side slip angle. These are used as look-up tables for computing the forces and the moments. | Both the magnitude and direction of the incoming air stream affect the resulting forces and moments so the angle of attack and side slip angles for the effective relative wind are computed. Configuration parameters of the fuselage includes two curves for each force and moment. One of them bases on angle of attack and the other on side slip angle. These are used as look-up tables for computing the forces and the moments. | ||
[[Image:RLIBDOC08.jpg|thumb|center|800px|Figure 6.7 Forces acting on the fuselage]] | |||
==== | ==== FGHeliFuselage100 configuration format ==== | ||
Simplified layout of the model configuration is provided below. | Simplified layout of the model configuration is provided below. | ||
| Line 339: | Line 327: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Fuselage | ===== Fuselage ===== | ||
CoPX CoPY CoPZ: Position of center of pressure relative to the fuselage center of gravity. These parameters are in meters. | |||
CoPX CoPY CoPZ : Position of center of pressure relative to the fuselage center of gravity. These parameters are in meters. | |||
====== MainRotorDownwash and MainRotorInplanewash ===== | |||
Each of these sections contain three curves which define the relationship between the induced velocity acting on the fuselage and the induced velocity of the main rotor. MainRotorDownwash is used to compute Cdownwash and MainRotorInplanewash is used to compute Cinplanewash. These are used to compute the rotorwash acting on the fuselage as follows: | Each of these sections contain three curves which define the relationship between the induced velocity acting on the fuselage and the induced velocity of the main rotor. MainRotorDownwash is used to compute Cdownwash and MainRotorInplanewash is used to compute Cinplanewash. These are used to compute the rotorwash acting on the fuselage as follows: | ||
* Downwash (positive downwards) = Main Rotor Induced Velocity * Cdownwash | |||
Downwash (positive downwards) = Main Rotor Induced Velocity * Cdownwash | * Inplanewash (positive backwards) = Main Rotor Induced Velocity * Cinplanewash | ||
Inplanewash (positive backwards) = Main Rotor Induced Velocity * Cinplanewash | |||
MainRotorDownwash and MainRotorInplanewash can contain three curves for three different a1 (main rotor longitudinal flapping in degrees) values. Depending on current a1, two nearest curves are selected and the coefficients for the current wake skew angle are looked up. Final coefficient is found by linear interpolation between the look-up values. | MainRotorDownwash and MainRotorInplanewash can contain three curves for three different a1 (main rotor longitudinal flapping in degrees) values. Depending on current a1, two nearest curves are selected and the coefficients for the current wake skew angle are looked up. Final coefficient is found by linear interpolation between the look-up values. | ||
Force curves ( Lift, Drag and Side force due to angle of attack and side slip ) | ====== Force curves (Lift, Drag and Side force due to angle of attack and side slip) ====== | ||
These curves contain lift, drag and side force coefficients depending on angle of attack and side slip. Coefficients due to angle of attack and side slip are found by using these curves as look-up tables. An example computation is provided below: | These curves contain lift, drag and side force coefficients depending on angle of attack and side slip. Coefficients due to angle of attack and side slip are found by using these curves as look-up tables. An example computation is provided below: | ||
* Clift = Cliftaoa + Cliftsideslip | |||
* Lift = dynamic pressure * Clift | |||
====== Moment curves (Pitching, yawing and rolling moments due to angle of attack and side slip) ====== | |||
Moment curves (Pitching, yawing and rolling moments due to angle of attack and side slip) | |||
These curves contain pitching moment, yawing moment and rolling moment coefficients depending on angle of attack and side slip. Coefficients due to angle of attack and side slip are found by using these curves as look-up tables. An example computation is provided below: | These curves contain pitching moment, yawing moment and rolling moment coefficients depending on angle of attack and side slip. Coefficients due to angle of attack and side slip are found by using these curves as look-up tables. An example computation is provided below: | ||
* Cpitch = Cpitchaoa + Cpitchsideslip | |||
* PitchingMoment = dynamics pressure * Cpitch | |||
=== Stabilizers === | === Stabilizers === | ||
Stabilizers are simulated with | Stabilizers are simulated with ''FGHelicopterStabilizerWing'' class. It is derived from ''FGWing'' and inherits most of the functionality from it. It extends ''FGWing'' by adding downwash and dynamic pressure change effects. | ||
[[Image:RLIBDOC09.jpg]] | [[Image:RLIBDOC09.jpg|thumb|center|800px|Figure 6.8 FGHelicopterStabilizerWing model inputs and outputs]] | ||
==== | ==== FGHelicopterStabilizerWing configuration ==== | ||
GenHeli500 allows definition of one vertical and two horizontal stabilizers. The definitions of the stabilizers are made in <VerticalStabilizer>, <HorizontalStabilizerRight> and <HorizontalStabilizerLeft> sections in the configuration file. Simplified layout of the configuration is provided below. | GenHeli500 allows definition of one vertical and two horizontal stabilizers. The definitions of the stabilizers are made in <VerticalStabilizer>, <HorizontalStabilizerRight> and <HorizontalStabilizerLeft> sections in the configuration file. Simplified layout of the configuration is provided below. | ||
| Line 466: | Line 444: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Geometry | ===== Geometry ===== | ||
* Position: Position of the aerodynamic center of the wing with respect to the aircraft CoG in meters. In RTDynamics coordinate system. | |||
Position : Position of the aerodynamic center of the wing with respect to the aircraft CoG in meters. In RTDynamics coordinate system. | * Up: A vector which determines the up direction of the wing in aircraft body coordinate system. | ||
* Front: A vector which determines the direction of the front in aircraft body coordinate system. | |||
Up : A vector which determines the up direction of the wing in aircraft body coordinate system. | * SurfaceArea | ||
** area: Wing surface area in square meters. | |||
Front : A vector which determines the direction of the front in aircraft body coordinate system. | |||
SurfaceArea | |||
area : Wing surface area in square meters. | |||
===== AerodynamicFeatures ===== | |||
====== DynamicPressureRatio ====== | |||
It is possible that due to interference with the fuselage, dynamic pressure observed at the stabilizers are different than the one which is computed using air density and the velocity. This effect is simulated using curves which contain the dynamic pressure ratio vs. fuselage angle of attack and side slip angles. Following equation is used: | It is possible that due to interference with the fuselage, dynamic pressure observed at the stabilizers are different than the one which is computed using air density and the velocity. This effect is simulated using curves which contain the dynamic pressure ratio vs. fuselage angle of attack and side slip angles. Following equation is used: | ||
* Stabilizer Dynamic Pressure = Dynamic Pressure * RatioAoA * RatioSideslip | |||
Stabilizer Dynamic Pressure = Dynamic Pressure * RatioAoA * RatioSideslip | |||
Here RatioAoA is looked up from <AoA> section (angles in degrees, ratio unitless), and RatioSideslip from <sideslip> (angles in degrees, ratio unitless) sections. | Here RatioAoA is looked up from <AoA> section (angles in degrees, ratio unitless), and RatioSideslip from <sideslip> (angles in degrees, ratio unitless) sections. | ||
MainRotorDownwash and MainRotorInplanewash | ====== MainRotorDownwash and MainRotorInplanewash ====== | ||
Each of these sections contain three curves which define the relationship between the induced velocity acting on the stabilizer and the induced velocity of the main rotor. MainRotorDownwash is used to compute Cdownwash and MainRotorInplanewash is used to compute Cinplanewash. These are used to compute the rotorwash acting on the stabilizer as follows: | Each of these sections contain three curves which define the relationship between the induced velocity acting on the stabilizer and the induced velocity of the main rotor. MainRotorDownwash is used to compute Cdownwash and MainRotorInplanewash is used to compute Cinplanewash. These are used to compute the rotorwash acting on the stabilizer as follows: | ||
* Downwash (positive downwards) = Main Rotor Induced Velocity * Cdownwash | |||
* Inplanewash (positive backwards) = Main Rotor Induced Velocity * Cinplanewash | |||
MainRotorDownwash and MainRotorInplanewash can contain three curves for three different a1 (main rotor longitudinal flapping in degrees) values. Depending on current a1, two nearest curves are selected and the coefficients for the current wake skew angle are looked up. Final coefficient is found by linear interpolation between the look-up values. | |||
====== LiftCurve and DragCurve ====== | |||
These curves contain the coefficient of lift and drag vs. angle of attack. Coefficients are unitless and angle of attack is in degrees. | |||
=== Engine and Drive Train === | === Engine and Drive Train === | ||
| Line 515: | Line 484: | ||
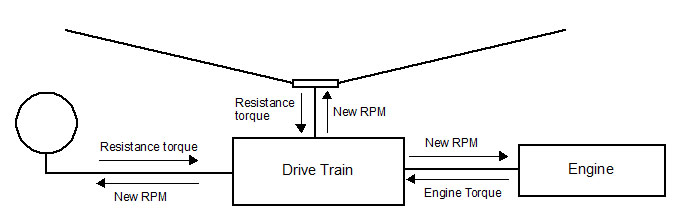
Following figure provides an overview of RotorLib's engine and transmission model. The central component of the model is the transmission which receives the torques as input and computes the final RPM's of the rotors and the engine shaft. The resistance torques applied by the rotors to the transmission are the torques generated by the air resistance on the rotor blades. The engine torque shown in the figure is the torque produced by the engine to rotate the rotors. Transmission uses these torques and the information about rotor gear ratios and rotor rotational inertias to compute angular accelerations and finally the final RPM's for the current frame. | Following figure provides an overview of RotorLib's engine and transmission model. The central component of the model is the transmission which receives the torques as input and computes the final RPM's of the rotors and the engine shaft. The resistance torques applied by the rotors to the transmission are the torques generated by the air resistance on the rotor blades. The engine torque shown in the figure is the torque produced by the engine to rotate the rotors. Transmission uses these torques and the information about rotor gear ratios and rotor rotational inertias to compute angular accelerations and finally the final RPM's for the current frame. | ||
[[Image:RLIBDOC10.jpg|thumb|center|800px|Figure 6.9 RotorLib engine and transmission model overview]] | |||
[[Image:RLIBDOC10.jpg]] | |||
It is important to note that the engine does not update its own RPM. Engines and rotors provide only the torques acting on the system. Angular accelerations and hence the final RPM's are computed by the transmission model by solving an equation system where solutions for all variables are found simultaneously. | It is important to note that the engine does not update its own RPM. Engines and rotors provide only the torques acting on the system. Angular accelerations and hence the final RPM's are computed by the transmission model by solving an equation system where solutions for all variables are found simultaneously. | ||
| Line 533: | Line 500: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
Performance | ===== Performance ===== | ||
Performance characteristics of the engine. | Performance characteristics of the engine. | ||
maxPower : Maximum power available at sea level. As the density altitude increases available power decreases. | * maxPower: Maximum power available at sea level. As the density altitude increases available power decreases. | ||
===== ControllerParams ===== | |||
A PID controller is used to regulate the engine torque output. These are parameters of this controller. | A PID controller is used to regulate the engine torque output. These are parameters of this controller. | ||
P : Proportional coefficient of the controller. | * P: Proportional coefficient of the controller. | ||
* I: Integral coefficient of the controller. | |||
I : Integral coefficient of the controller. | * D: Derivative coefficient of the controller. | ||
* offset: "Zero point" of the controller. When error, error derivative and error sum is zero resulting value will be offset. | |||
D : Derivative coefficient of the controller. | * targetRPM: The engine shaft RPM the controller will try to reach. | ||
=== Automatic flight control system === | === Automatic flight control system === | ||
| Line 566: | Line 529: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
More info about | More info about the [http://en.wikipedia.org/wiki/PID_controller|'''PID controler''' concept] | ||
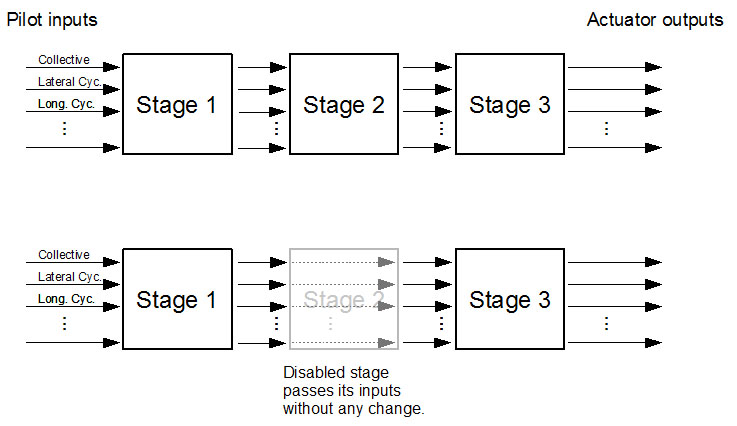
If multiple components are defined in the configuration, they are connected to each other in a cascade, i.e. each stage receives its inputs from the previous stage. Only the first stage receives its inputs directly from the pilot. A disabled stage passes its inputs to the next stage without any change. By enabling/disabling the stages, different automatic control system configurations can be obtained. If all stages are disabled, pilot inputs directly control the actuators. | If multiple components are defined in the configuration, they are connected to each other in a cascade, i.e. each stage receives its inputs from the previous stage. Only the first stage receives its inputs directly from the pilot. A disabled stage passes its inputs to the next stage without any change. By enabling/disabling the stages, different automatic control system configurations can be obtained. If all stages are disabled, pilot inputs directly control the actuators. | ||
[[Image:RLIBDOC11.jpg|thumb|center|800px|Figure 6.10 Overview of control system model]] | |||
[[Image:RLIBDOC11.jpg]] | |||
==== RTD::FCSRotationDamper ==== | ==== RTD::FCSRotationDamper ==== | ||
| Line 585: | Line 546: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
YawController | ===== YawController ===== | ||
Configures the PD controller that damps yawing motion. | |||
* P: Proportional coefficient of the controller. | |||
* D: Derivative coefficient of the controller. | |||
===== PitchController ===== | |||
Configures the PD controller that damps pitching motion. | |||
* P: Proportional coefficient of the controller. | |||
* D: Derivative coefficient of the controller. | |||
===== RollController ===== | |||
Configures the PD controller that damps rolling motion. | |||
* P: Proportional coefficient of the controller. | |||
* D: Derivative coefficient of the controller. | |||
=== RotorLibFDM::FCSHelicopterAutoTrim === | |||
This control system component is used to trim the helicopter automatically and hence remove the coupling between controls (i.e. collective / pedal coupling). It translates pilot inputs to requested heading, pitch and roll rates or to requested side slip and controls the actuators to achieve the desired state. The final result is a simpler flight. | |||
''FCSHelicopterAutoTrim'' is suitable for simulators where simple input devices, such as a joystick, is used. In case real helicopter input devices with trim lock controls are used, ''FCSHelicopterAutoTrim'' should not be used. | |||
<syntaxhighlight lang="xml"> | |||
<FSComponent type="FCSHelicopterAutoTrim"> | |||
<YawRateAndSideslipController printDebugInfo> | |||
<YawRatePID P I D offset integralMin integralMax /> | |||
<SideslipPID P I D offset integralMin integralMax /> | |||
<Transition speedLow speedHigh /> | |||
<Maximums maxYawRate maxSideslip /> | |||
<InputMapping nonlinearity /> | |||
</YawRateAndSideslipController> | |||
<PitchRateController printDebugInfo > | |||
<PID P I D offset integralMin integralMax /> | |||
<MaxPitchRate maxPitchRate /> | |||
</PitchRateController> | |||
<RollRateController printDebugInfo > | |||
<PID P I D offset integralMin integralMax /> | |||
<MaxRollRate maxRollRate /> | |||
</RollRateController> | |||
<FSComponent type="FCSHelicopterAutoTrim"> | |||
</syntaxhighlight> | |||
===== YawRateAndSideslipController ===== | |||
This controller controls the pedals to reach and maintain a certain yaw rate or side slip. Yaw rate control mode is active at low speeds, whereas side slip control mode is activated at high speeds. The mode change occurs smoothly within a user defined speed range (see Transition below). Within this transition region, both yaw rate and side slip control modes are active but their contribution to the final output varies depending on speed. | |||
====== printDebugInfo ====== | |||
A boolean parameter (possible values "true" and "false" ) to enable/disable debug output to the console from the controller. This is useful for the parametrization of the controller. | |||
D : Derivative coefficient of the controller. | * YawratePID: Parameters of the PID controller that is used to control yaw rate. Error input to this PID is desired yaw rate - current yaw rate. Desired yaw rate is determined by the pedal input, i.e. pilot's pedal input is translated to a desired yaw rate by the controller. | ||
** P: Proportional coefficient of the controller. | |||
** I: Integral coefficient of the controller. | |||
** D: Derivative coefficient of the controller. | |||
** offset: "Zero point" of the controller. When error, error derivative and error sum is zero resulting value will be offset. | |||
** IntegralMin and integralMax: Minimum/Maximum value the error sum can reach. If the sum of errors go below/above this value it is clamped to this value. | |||
* SideslipPID: Parameters of the PID controller that is used to control side slip. Error input to this PID is desired side slip - current side slip. Desired side slip is determined by the pedal input, i.e. pilot's pedal input is translated to a desired side slip by the controller. | |||
** P: Proportional coefficient of the controller. | |||
** I: Integral coefficient of the controller. | |||
** D: Derivative coefficient of the controller. | |||
** offset: "Zero point" of the controller. When error, error derivative and error sum is zero resulting value will be offset. | |||
** IntegralMin and integralMax: Minimum/Maximum value the error sum can reach. If the sum of errors go below/above this value it is clamped to this value. | |||
* Transition: YawRateAndSideslipController is designed so that it interprets the pilot pedal input as desired yaw rate at low speeds and as desired side slip at high speeds. A transition region based on speed can be defined to enable a smooth transition between these modes. | |||
** speedLow and speedHigh : Below speedLow, the pedal input will be interpreted as desired yaw rate and after speedHigh as desired side slip. Between these two speeds, the outputs of the Yaw Rate and Side slip subcontrollers will be linearly mixed. | |||
* Maximums | |||
** maxYawRate: Maximum yaw rate that can be requested from the controller. This parameter is in deg/s and must be positive always. | |||
** maxSideslip: Maximum side slip angle that can be requested from the controller. This parameter is in degrees and must be positive always. | |||
* InputMapping | |||
** nonlinearity : In some cases, it might be better to pass the pilot input to the control system non-linearly. For example, in a desktop simulator, where the input device is a common joystick, we might want to have a better precision at the zero point. We can define an exponential relationship between pilot's input and the control system input using nonlinearity parameter. The pedal input that is given to the control system is computed as follows: pedal input to controller = (|pilot pedal input| ^ nonlinearity) * sign(pilot pedal input). | |||
===== PitchRateController, RollRateController ====== | |||
Controllers for pitch and roll rates. | |||
* PID: Parameters of the PID controller that is used to regulate the rotational motion. | |||
** P: Proportional coefficient of the controller. | |||
** I: Integral coefficient of the controller. | |||
** D: Derivative coefficient of the controller. | |||
** offset: "Zero point" of the controller. When error, error derivative and error sum is zero resulting value will be offset. | |||
** IntegralMin and integralMax: Minimum/Maximum value the error sum can reach. If the sum of errors go below/above this value it is clamped to this value. | |||
* MaxPitchRate and MaxRollRate: These are maximum angular speeds the controllers are trying to reach. E.g. if control stick is pulled 100% right, RollRateController will try to reach a roll rate of maxRollRate. The values are in deg/sec. | |||
* InputMapping | |||
** nonlinearity : In some cases, it might be better to pass the pilot input to the control system non-linearly. For example, in a desktop simulator, where the input device is a common joystick, we might want to have a better precision at the zero point. We can define an exponential relationship between pilot's input and the control system input using nonlinearity parameter. The actual input that is given to the control system is computed as follows: input to controller = (|pilot input| ^ nonlinearity) * sign(pilot input). | |||
=== Ground contacts === | === Ground contacts === | ||
| Line 627: | Line 658: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
===== GeneralConfiguration ===== | |||
* gearExtensionTime: Time needed to extend/retract landing gears in seconds. | |||
* gearDragCoefficient: Coefficient of drag for landing gears. | |||
* gearReferenceArea: Reference area of the landing gears to be used in air drag computation. | |||
* maxSteerableGearDeflection: Maximum deflection (in degrees) of the steerable gears. | |||
* steerableGearSpeedCorrectionFactor: As the speed of the aircraft increases, deflections of steerable gears are automatically reduced to keep the aircraft controllable. This parameter defines the strength of this correction. | |||
===== GroundContact ===== | |||
A multitude of <GroundContact> </GroundContact> sections can be defined. The type parameter defines which ground contact model (E.g. FGGroundContact200) has to be used. Inside the opening and closing tags, configuration parameters of the chosen model has to be provided. | |||
GroundContact | |||
A multitude of <GroundContact> </GroundContact> sections can be defined. The type parameter defines which ground contact model (E.g. FGGroundContact200 ) has to be used. Inside the opening and closing tags, configuration parameters of the chosen model has to be provided. | |||
==== FGGroundContact200 configuration ==== | ==== FGGroundContact200 configuration ==== | ||
| Line 673: | Line 696: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
===== Features ===== | |||
Features | |||
General features of the ground contact. | General features of the ground contact. | ||
isBrakable : Is the ground contact a brakable landing gear? (true or false) | * isBrakable: Is the ground contact a brakable landing gear? (true or false) | ||
* isRetractable: Is the ground contact a retractable landing gear? (true or false) | |||
isRetractable : Is the ground contact a retractable landing gear? (true or false) | * isSteerable: Is the ground contact a steerable landing gear? (true or false) | ||
isSteerable : Is the ground contact a steerable landing gear? (true or false) | |||
===== Suspension ===== | |||
Parameters of the suspension. | Parameters of the suspension. | ||
MountStation : Position at which the landing gear is mounted onto the aircraft body. Relative to center of gravity and in meters. | * MountStation: Position at which the landing gear is mounted onto the aircraft body. Relative to center of gravity and in meters. | ||
* SliderAxis: This is a unit direction vector which determines along which direction suspension slider can move. It is defined relative to aircraft body coordinates in RTDDynamics coordinate system convention. | |||
SliderAxis : This is a unit direction vector which determines along which direction suspension slider can move. It is defined relative to aircraft body coordinates in RTDDynamics coordinate system convention. | * SuspensionLength: Length of the suspension, i.e. the distance from mount station to middle point of wheel when suspensions are not compressed or decompressed. In meters. | ||
* SpringParameters | |||
SuspensionLength : Length of the suspension, i.e. the distance from mount station to middle point of wheel when suspensions are not compressed or decompressed. In meters. | ** springConstant: Spring constant of the suspension spring. In N/m. | ||
** damperConstant: Damper constant of the suspension spring. In N*sec/meter. | |||
SpringParameters | ** maxCompression: Maximum amount the suspension spring can be compressed. This value should be less than or equal to suspension length. In meters. | ||
springConstant : Spring constant of the suspension spring. In N/m. | |||
damperConstant: Damper constant of the suspension spring. In N*sec/meter. | |||
maxCompression : Maximum amount the suspension spring can be compressed. This value should be less than or equal to suspension length. In meters. | |||
===== Wheel ===== | |||
Parameters of the wheel. | Parameters of the wheel. | ||
mass : Mass in Kg. | * mass: Mass in Kg. | ||
* radius: Radius of the wheel in meters. | |||
* rotationalInertia: Rotational inertia of the wheel in Kg*m^2. | |||
** RollAxis: A direction vector that defines the axis of wheel rotation. It is defined relative to aircraft body coordinates. | |||
** Friction | |||
*** slidingFriction: Coefficient of friction between the tire and the ground. | |||
*** resistanceTorqueNoBrake and resistanceTorqueFullBrake: An effective resistance torque from linear interpolation of resistanceTorqueNoBrake and resistanceTorqueFullBrake depending on the amount of applied wheel brake is applied to the wheel continuously to simulate rolling friction. The resistance torque acts in a direction that opposes the current rotation of the wheel. In N*m. | |||
===== SteeringController ===== | |||
* maxTorque: The steering controller rotates the wheel left or right depending on the pilot's input for steering on the ground. This parameter defines how much torque can be applied to the wheel for this purpose. This parameter is in N*m. | |||
* maxRotSpeed: This parameter defines how fast the wheel can rotate around the vertical axis. In Deg/sec. | |||
* controllerGain: The torque applied to the wheel to rotate it is proportional to the difference of pilot's desired wheel direction and current direction multiplied by \e m_steeringControllerGain (the result is clamped at \e m_steeringMaxTorque ). This parameter is unitless. | |||
* inverseRotation: If this parameter is set to true, the wheel will rotate in the opposite direction of the pilot input (if pilot input is to the right wheel will rotate to the left etc. ). This is necessary if the steering wheel is at the back instead of front. | |||
* keepCenter: If this parameter is set to true, the wheel will not be affected by the pilot's control input but instead will try to keep the wheel in center always. This is useful to model free rotating wheels (a wheel that can rotate around vertical axis but is not actively controlled by actuators ). | |||
===== Damage ===== | |||
* thresholdLoad: During landing the forces acting on the wheel are transferred to the fuselage. Beyond a certain threshold the transferred forces result in damage in the aircraft. The load defined in thresholdLoad (in N) is the threshold used for this purpose. | |||
[[Category: Take On Helicopters: Editing]] | |||
Revision as of 15:31, 21 November 2011
Disclaimer
This documentation was reproduced from the official RotorLib Programmer's Guide with permission from RTDynamics.
Please note that this version of the documentation (3.2) is based on a slightly older version of the library than the one used in TKOH (3.3). As soon as updated official documentation becomes available, we'll update this resource.
What is RotorLib FDM?
RotorLib FDM is RTDynamics' rotary wing aircraft flight dynamics model solution. It includes aerodynamic models, ground contact model, flight instrument models and flight control system simulation.
RotorLib FDM is designed for pilot-in-the-loop applications such as flight training simulators, mission rehearsal systems and combat training simulators.
RotorLib Flight Dynamics Model
GenHeli500 model
The generic RotorLib FDM helicopter flight dynamics model is implemented in RotorLibFDM::GenHeli500 class. This class uses several mathematical models as components to create a generic helicopter model. GenHeli500 consists of:
- one main rotor and one tail rotor (both based on FGRotorMomentumTheory model)
- vertical and horizontal stabilizers ( based on FGHelicopterStabilizerWing )
- fuselage model ( FGHeliFuselage100 )
- a user defined number of ground contacts which can be configured as steerable or non-steerable gears and body contacts .
- extensible engine model
- drive train model
- extensible flight control system
- flight instruments
Forces and moments computed by models above are used by a real-time rigid body dynamics model to update the rigid body state of the helicopter. Below you can find an overview of the rigid body dynamics used in RotorLib.
GenHeli500 configuration
GenHeli500 flight dynamics model is configured through XML configuration files. These configuration files are given to the constructor of the GenHeli500 class.
Configuration files start with an FDM type declaration and file version definition. Configuration parameters are defined between the opening and closing tags of this type declaration. The simplified layout of the configuration is provided below.
<GenHeli500 version="1.0">
<MomentsOfInertia Ixx Iyy Izz Iyz />
<Mass mass/>
<Fuselage>
--> Fuselage parameters <--
</Fuselage>
<Engines>
<Engine type>
--> Engine parameters <--
</Engine>
</Engines>
<ControlSystem>
<FCSComponent type >
--> Flight contol system component parameters <--
</FCSComponent>
.
.
.
<FCSComponent type >
--> Flight contol system component parameters <--
</FCSComponent>
</ControlSystem>
<MainRotor>
--> Main rotor parameters <--
</MainRotor>
<TailRotor>
--> Tail rotor parameters <--
</TailRotor>
<HorizontalStabilizerRight>
--> Right horizontal stabilizer parameters <--
</HorizontalStabilizerRight>
<HorizontalStabilizerLeft>
--> Left horizontal stabilizer parameters <--
</HorizontalStabilizerLeft>
<VerticalStabilizer>
--> Vertical stabilizer parameters <--
</VerticalStabilizer>
<GroundContacts>
<GeneralConfiguration
gearExtensionTime gearDragCoefficient
gearReferenceArea maxSteerableGearDeflection
maxSteerableGearDeflection
steerableGearSpeedCorrectionFactor/>
<GroundContact type>
--> Ground contact parameters <--
</GroundContact>
.
.
.
<GroundContact type>
--> Ground contact parameters <--
</GroundContact>
</GroundContacts>
</GenHeli500>
- MomentsOfInertia - Moments of inertia of the helicopter body are defined here. Available parameters are Ixx, Iyy, Izz and Iyz (in Kg*m^2)
- Mass - mass parameter defines the mass of the helicopter in Kg.
- Fuselage - GenHeli500 fuselage model is implemented using RotorLibFDM::FGHeliFuselage100 model. See Fuselage section below for details.
- Engines - In this section, engines are configured. Configuration for the chosen engine model must be provided inside the <Engine> </Engine> tags.
- ControlSystem - Automatic flight control system configuration. In this section a multitude of flight control system components can be defined. Each component should be defined in a separate <FCSComponent> section. type parameter in FCSComponent defines which component type (e.g. FCSRotationDamper ) will be created. Inside the <FCSComponent> </FCSComponent> configuration parameters of the chosen component model has to be provided.
- MainRotor and TailRotor - In these sections main and tail rotors are configured. Rotors use RTD::FGRotorMomentumTheory rotor model. See Rotor model section for details.
- HorizontalStabilizerRight, HorizontalStabilizerLeft and VerticalStabilizer - Stabilizers use RTD::FGHelicopterStabilizerWing wing model. See Stabilizers section for details.
- GroundContacts - In this section ground contacts of the helicopter are configured. See Ground Contacts section for details.
Rotor Model
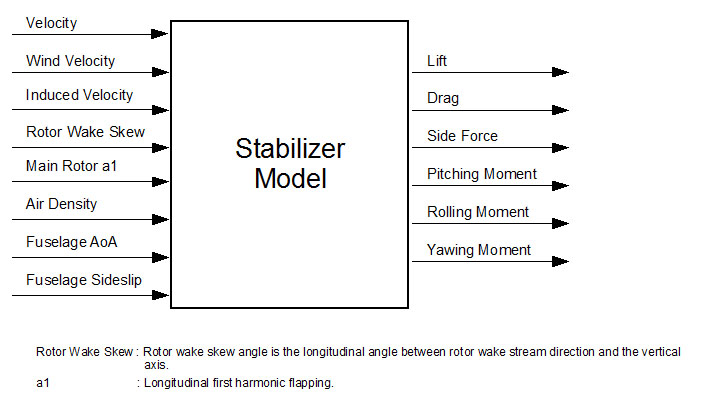
GenHeli500 uses FGRotorMomentumTheory class as rotor model. This class simulates aerodynamic and mechanical behavior of a rotor. It is used for both main and tail rotors. FGRotorMomentumTheory uses momentum theory and certain blade element theory elements to compute the forces and moments. It also outputs values, such as induced velocity or wake skew angle, that are used as input by other mathematical models, such as fuselage model. Inputs and outputs of the model are summarized below:
A helicopter rotor produces thrust by setting the air around it in motion. As a result, a rotor operates in the airflow which is induced by itself. Because of the induced airflow, rotor blades operate in a downward air stream which reduces the effective angle of attack which in turn results in reduced lift. In momentum theory of rotors, the law of conservation of momentum is used on the airflow and an equation that relates T (thrust produced by the rotor) to Vi (speed of the air stream at the rotor disc) is obtained. A second equation that relates T and Vi can be written with blade element theory. Resulting equations are not linear and they are not solvable with algebraic methods hence an iterative numerical solution is implemented.
Simulation update of the rotor model begins by solving above equations and finding T (Thrust) and Vi (induced velocity). Once we know T and Vi, H (Drag) and Y(Side force) are computed.
The next step in rotor update is updating flapping dynamics. A fully articulated helicopter rotor has flapping, lead-lag and feathering hinges. These hinges provide a certain amount of independent motion capability to the blades. Blades can lead and lag the rotation of the hub on the disc plane. Moreover, because of the flapping hinge, they can move below or above the disc plane. These extra degrees of freedom have effects on power consumption, forces, moments and handling quality. FGRotorMomentumTheory simulates first order flapping dynamics: It computes a1,b1and a0 (coning angle). Higher order terms in the flapping equation and the lead-lag motion is ignored since their effect on the rotor is less important compared to the first order flapping terms. See following figure for the details of the flapping equation and geometry.
After flapping dynamics, power is computed. Power is computed as a sum of following components:
- Induced power : Power consumption due to induced air flow.
- Parasite power : Power consumption due to the drag of fuselage, rotor hub, external stores etc.
- Climbing power : Power consumption/gain due to altitude change (potential energy change).
- Profile power : Power consumption due to blade profile drag.
By computing the power consumption of the rotor we also get information about the torque acting on the rotor shaft ( P = angular speed x torque ). This torque is the load the rotor is putting on the engine through the drive train, hence it is an input to the drive train model. Moreover, it also acts on the helicopter fuselage and tries to rotate it in the opposite direction of rotor and hence has effects on flight handling.
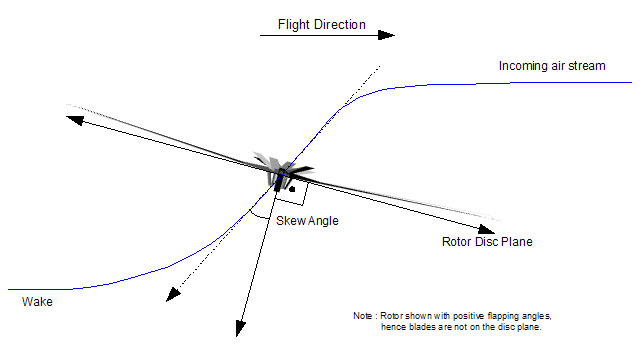
After power, moments at the CoG of the helicopter and rotor wake skew angle are computed. Rotor wake skew angle, along with Vi, is used by other components (fuselage, stabilizers and tail rotor) as input.
If the model is used to simulate a tail rotor, interference with main rotor and fuselage is taken into account in all above steps.
FGRotorMomentumTheory configuration format
To configure the main rotor, a <MainRotor> section must be defined in the configuration file. Configuration parameters of the rotor has to be in this section. For the tail rotor, <TailRotor> section must be used.
Simplified layout of the model configuration is provided below.
<MainRotor> <-- For tail rotor use <TailRotor>
<Geometry>
<Position x y z />
<Tilt lateralTilt longitudinalTilt />
<Blades radius chord count hingeOffset />
</Geometry>
<MechanicalFeatures Ir gearRatio Ib />
<AerodynamicFeatures>
<Blades liftCurveSlope zeroLiftDragCoefficient twist />
<Controls A1UL A1LL B1UL B1LL thetaLL thetaUL />
<Power inducedPowerCorrectionFactor />
<GroundEffect magnitude />
<DesignRPM rpm/>
</AerodynamicFeatures>
</MainRotor>
Geometry
This section defines the rotor geometry. All vectors are in RTDynamics coordinate system ( Y forward, X rightward, Z up). They are defined relative to the helicopter body coordinate system.
- Position: position of the rotor hub relative to the center of gravity of the helicopter. In meters.
- Tilt: orientation of the rotor.
- lateralTilt: Lateral tilt of the rotor in degrees. Positive values denote a rightward tilt.
- longitudinalTilt: Longitudinal tilt of the rotor in degrees. Positive values denote a backward tilt. This parameter is negative for most of the helicopters.
- Blades: Blade parameters.
- count: Number of blades.
- radius: Radius of the blades in meters.
- chord: Chord (width) of the blades in meters.
- hingeOffset: Distance of the flapping hinge from rotation center in meters.
MechanicalFeatures: Mechanical features of the rotor
- Ir: Moment of inertia (rotational inertia) of the rotor about the axis of rotation. In kg*m^2.
- Ib: Moment of inertia (rotational inertia) of a blade about the flapping hinge. In kg*m^2.
- gearRatio: Gear ratio between the engine and the rotor. rotor RPM = engine RPM / gearRatio.
AerodynamicFeatures
- Blades
- liftCurveSlope: Slope of the blade lift curve. X axis of the curve is assumed to be in degrees. This parameter does not have a unit. Example: If a lift curve has Clmax = 1.5 at 15 degrees , liftCurveSlope will be 1.5/15 = 0.1.
- zeroLiftDragCoefficient: Drag coefficient of the blades at zero lift. This parameter does not have a unit.
- twist: Blade twist in degrees.
- Controls
- A1UL: Upper limit of lateral swash plate tilt in degrees.
- A1LL: Lower limit of lateral swash plate tilt in degrees.
- B1UL: Upper limit of longitudinal swash plate tilt in degrees.
- B1LL: Lower limit of longitudinal swash plate tilt in degrees.
- thetaLL: Minimum pitch of the blades due to collective input. When collective input is 0 blade pitch will be thetaLL degrees.
- thetaUL: Maximum pitch of the blades due to collective input. When collective input is 1 blade pitch will be thetaUL degrees.
- Power
inducedPowerCorrectionFactor: Due to various reasons, momentum theory requires an empirical correction factor for the computation of the induced power. This parameter is used for this purpose.
- DesignRPM
- rpm: Design RPM of the rotor. If no engine is connected to the helicopter, rotor will rotate with this speed. In revolutions per minute.
- GroundEffect
- magnitude: An empirical parameter which defines the magnitude of the ground effect. This parameter does not have a unit.
Fuselage
Fuselage model is implemented in FGHeliFuselage100 class. Inputs and outputs of the model are summarized in the following diagram:
All forces and moments are computed at the center of gravity.
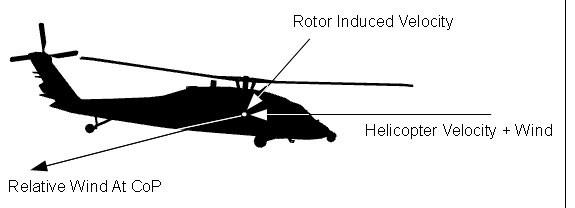
During simulation update, fuselage model initially computes the effective relative wind (in other words, air stream velocity) acting on the fuselage. To compute the effective relative wind helicopter velocity, wind velocity and the main rotor downwash is used. Downwash is characterized by rotor wake skew angle and induced velocity, which are outputs of the rotor model (see Rotor model section for details). Unfortunately, these values can not be used directly to compute the rotor's effect on the fuselage because they are only reference values and the actual induced velocity changes depending on the position on the helicopter. Different parts of the fuselage receive different amount of induced air stream. Therefore there are two curve sets in the configuration file ( MainRotorDownwash and MainRotorInplanewash) which define downwash and inplanewash coefficients depending on the rotor wake skew angle. Using induced velocity output of the main rotor and these curves (as look-up tables indexed by rotor wake angle) final air stream velocity vector is computed.
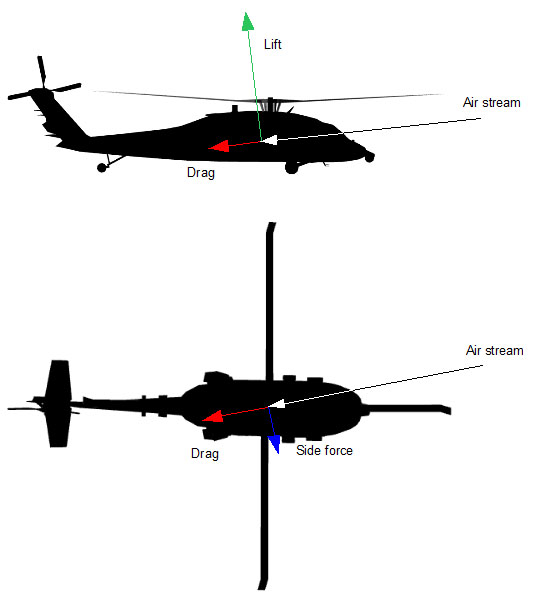
Both the magnitude and direction of the incoming air stream affect the resulting forces and moments so the angle of attack and side slip angles for the effective relative wind are computed. Configuration parameters of the fuselage includes two curves for each force and moment. One of them bases on angle of attack and the other on side slip angle. These are used as look-up tables for computing the forces and the moments.
FGHeliFuselage100 configuration format
Simplified layout of the model configuration is provided below.
<Fuselage CoPX CoPY CoPZ>
<MainRotorInplanewash>
<Low_a1 a1>
WakeSkewAngle_1 Cinplanewash_1
WakeSkewAngle_2 Cinplanewash_2
.
.
.
WakeSkewAngle_n Cinplanewash_n
</Low_a1>
<Medium_a1 a1>
--> As in Low_a1 <--
</Medium_a1>
<High_a1 a1>
--> As in Low_a1 <--
</High_a1>
</MainRotorInplanewash>
<MainRotorDownwash>
<Low_a1 a1>
WakeSkewAngle_1 Cdownwash_1
WakeSkewAngle_2 Cdownwash_2
.
.
.
WakeSkewAngle_n Cdownwash_n
</Low_a1>
<Medium_a1 a1>
--> As in Low_a1 <--
</Medium_a1>
<High_a1 a1>
--> As in Low_a1 <--
</High_a1>
</MainRotorDownwash>
<LiftDueToAoA>
AngleOfAttack_1 Cliftaoa_1
AngleOfAttack_2 Cliftaoa_2
.
.
.
AngleOfAttack_n Cliftaoa_n
</LiftDueToAoA>
<LiftDueToSideslip>
SideSlip_1 Cliftsideslip_1
SideSlip_2 Cliftsideslip_2
.
.
.
SideSlip_n Cliftsideslip_n
</LiftDueToSideslip>
<SideForceDueToAoA>
--> Similar to LiftDueToAoA <--
</SideForceDueToAoA>
<SideForceDueToSideslip>
--> Similar to LiftDueToSideslip <--
</SideForceDueToSideslip>
<DragDueToAoA>
--> Similar to LiftDueToAoA <--
</DragDueToAoA>
<DragDueToSideslip>
--> Similar to LiftDueToSideslip <--
</DragDueToSideslip>
<PitchingMomentDueToAoA>
--> Similar to LiftDueToAoA <--
</PitchingMomentDueToAoA>
<PitchingMomentDueToSideslip>
--> Similar to LiftDueToSideslip <--
</PitchingMomentDueToSideslip>
<RollingMomentDueToAoA>
--> Similar to LiftDueToAoA <--
</RollingMomentDueToAoA>
<RollingMomentDueToSideslip>
--> Similar to LiftDueToSideslip <--
</RollingMomentDueToSideslip>
<YawingMomentDueToAoA>
--> Similar to LiftDueToAoA <--
</YawingMomentDueToAoA>
<YawingMomentDueToSideslip>
--> Similar to LiftDueToSideslip <--
</YawingMomentDueToSideslip>
</Fuselage>
Fuselage
CoPX CoPY CoPZ: Position of center of pressure relative to the fuselage center of gravity. These parameters are in meters.
= MainRotorDownwash and MainRotorInplanewash
Each of these sections contain three curves which define the relationship between the induced velocity acting on the fuselage and the induced velocity of the main rotor. MainRotorDownwash is used to compute Cdownwash and MainRotorInplanewash is used to compute Cinplanewash. These are used to compute the rotorwash acting on the fuselage as follows:
- Downwash (positive downwards) = Main Rotor Induced Velocity * Cdownwash
- Inplanewash (positive backwards) = Main Rotor Induced Velocity * Cinplanewash
MainRotorDownwash and MainRotorInplanewash can contain three curves for three different a1 (main rotor longitudinal flapping in degrees) values. Depending on current a1, two nearest curves are selected and the coefficients for the current wake skew angle are looked up. Final coefficient is found by linear interpolation between the look-up values.
Force curves (Lift, Drag and Side force due to angle of attack and side slip)
These curves contain lift, drag and side force coefficients depending on angle of attack and side slip. Coefficients due to angle of attack and side slip are found by using these curves as look-up tables. An example computation is provided below:
- Clift = Cliftaoa + Cliftsideslip
- Lift = dynamic pressure * Clift
Moment curves (Pitching, yawing and rolling moments due to angle of attack and side slip)
These curves contain pitching moment, yawing moment and rolling moment coefficients depending on angle of attack and side slip. Coefficients due to angle of attack and side slip are found by using these curves as look-up tables. An example computation is provided below:
- Cpitch = Cpitchaoa + Cpitchsideslip
- PitchingMoment = dynamics pressure * Cpitch
Stabilizers
Stabilizers are simulated with FGHelicopterStabilizerWing class. It is derived from FGWing and inherits most of the functionality from it. It extends FGWing by adding downwash and dynamic pressure change effects.
FGHelicopterStabilizerWing configuration
GenHeli500 allows definition of one vertical and two horizontal stabilizers. The definitions of the stabilizers are made in <VerticalStabilizer>, <HorizontalStabilizerRight> and <HorizontalStabilizerLeft> sections in the configuration file. Simplified layout of the configuration is provided below.
<HorizontalStabilizerRight>
<Geometry>
<Position x y z />
<Up x y z />
<Front x y z />
<SurfaceArea area />
</Geometry>
<AerodynamicFeatures>
<DynamicPressureRatio>
<AoA>
AoA_1 ratio_1
AoA_2 ratio_2
.
.
.
AoA_n ratio_n
</AoA>
<Sideslip>
Sideslip_1 ratio_1
Sideslip_2 ratio_2
.
.
.
Sideslip_n ratio_n
</Sideslip>
</DynamicPressureRatio>
<MainRotorDownwash>
<Low_a1 a1>
WakeSkew_1 DownwashFactor1
WakeSkew_2 DownwashFactor2
.
.
.
WakeSkew_n DownwashFactorn
</Low_a1>
<Medium_a1 a1>
WakeSkew_1 DownwashFactor_1
WakeSkew_2 DownwashFactor_2
.
.
.
WakeSkew_n DownwashFactor_n
</Medium_a1>
<High_a1 a1>
WakeSkew_1 DownwashFactor_1
WakeSkew_2 DownwashFactor_2
.
.
.
WakeSkew_n DownwashFactor_n
</High_a1>
</MainRotorDownwash>
<MainRotorInplanewash>
--> As in MainRotorDownwash <--
</MainRotorInplanewash>
<LiftCurve>
AoA_1 Cl_1
AoA_2 Cl_2
.
.
.
AoA_n Cl_n
</LiftCurve>
<DragCurve >
AoA_1 Cd_1
AoA_2 Cd_2
.
.
.
AoA_n Cd_n
</DragCurve>
</AerodynamicFeatures>
</HorizontalStabilizerRight>
Geometry
- Position: Position of the aerodynamic center of the wing with respect to the aircraft CoG in meters. In RTDynamics coordinate system.
- Up: A vector which determines the up direction of the wing in aircraft body coordinate system.
- Front: A vector which determines the direction of the front in aircraft body coordinate system.
- SurfaceArea
- area: Wing surface area in square meters.
AerodynamicFeatures
DynamicPressureRatio
It is possible that due to interference with the fuselage, dynamic pressure observed at the stabilizers are different than the one which is computed using air density and the velocity. This effect is simulated using curves which contain the dynamic pressure ratio vs. fuselage angle of attack and side slip angles. Following equation is used:
- Stabilizer Dynamic Pressure = Dynamic Pressure * RatioAoA * RatioSideslip
Here RatioAoA is looked up from <AoA> section (angles in degrees, ratio unitless), and RatioSideslip from <sideslip> (angles in degrees, ratio unitless) sections.
MainRotorDownwash and MainRotorInplanewash
Each of these sections contain three curves which define the relationship between the induced velocity acting on the stabilizer and the induced velocity of the main rotor. MainRotorDownwash is used to compute Cdownwash and MainRotorInplanewash is used to compute Cinplanewash. These are used to compute the rotorwash acting on the stabilizer as follows:
- Downwash (positive downwards) = Main Rotor Induced Velocity * Cdownwash
- Inplanewash (positive backwards) = Main Rotor Induced Velocity * Cinplanewash
MainRotorDownwash and MainRotorInplanewash can contain three curves for three different a1 (main rotor longitudinal flapping in degrees) values. Depending on current a1, two nearest curves are selected and the coefficients for the current wake skew angle are looked up. Final coefficient is found by linear interpolation between the look-up values.
LiftCurve and DragCurve
These curves contain the coefficient of lift and drag vs. angle of attack. Coefficients are unitless and angle of attack is in degrees.
Engine and Drive Train
RotorLib FDM has an extensible engine model architecture. Engine models are classes that are derived from RTD::EngineModelBase. An existing or user-developed engine model can be attached to the helicopter by defining it in the XML configuration file. To create an engine, an <Engine> section should be defined and engine type has to be set. The configuration parameters of the engine should be between opening and closing tags of the section. Here is an example which creates and configures a ConstantRPMEngine.
<Engine type="ConstantRPMEngine">
<Performance maxPower="3000" />
<ControllerParams P="0.04" I="1.0" D="0.0"
offset="200" targetRPM="20900"/>
</Engine>
Following figure provides an overview of RotorLib's engine and transmission model. The central component of the model is the transmission which receives the torques as input and computes the final RPM's of the rotors and the engine shaft. The resistance torques applied by the rotors to the transmission are the torques generated by the air resistance on the rotor blades. The engine torque shown in the figure is the torque produced by the engine to rotate the rotors. Transmission uses these torques and the information about rotor gear ratios and rotor rotational inertias to compute angular accelerations and finally the final RPM's for the current frame.
It is important to note that the engine does not update its own RPM. Engines and rotors provide only the torques acting on the system. Angular accelerations and hence the final RPM's are computed by the transmission model by solving an equation system where solutions for all variables are found simultaneously.
ConstantRPMEngine
ConstantRPMEngine is a helicopter engine model provided with RotorLib library. This engine model has an internal control system that tries to keep the rotor RPM at a given rate. The controller determines the torque output for this purpose. It is possible to define the maximum power output of a ConstantRPMEngine. This power will be available at the sea level. ConstantRPMEngine computes the actual available power depending on density altitude. Configuration format of the model is below.
<Engine type="ConstantRPMEngine">
<Performance maxPower />
<ControllerParams P I D offset targetRPM/>
</Engine>
Performance
Performance characteristics of the engine.
- maxPower: Maximum power available at sea level. As the density altitude increases available power decreases.
ControllerParams
A PID controller is used to regulate the engine torque output. These are parameters of this controller.
- P: Proportional coefficient of the controller.
- I: Integral coefficient of the controller.
- D: Derivative coefficient of the controller.
- offset: "Zero point" of the controller. When error, error derivative and error sum is zero resulting value will be offset.
- targetRPM: The engine shaft RPM the controller will try to reach.
Automatic flight control system
RotorLib FDM has an extensible automatic flight control system architecture. Existing and/or user developed control system components can be attached to the helicopter and configured using XML configuration files. Control system components are created and configured in <ControlSystem> section of the configuration file. In this section, for each component ( in other words, for each stage ) a <FSComponent> subsection has to be defined and component type has to be set using type attribute. Following example defines a single stage of type FCSRotationDamper:
<ControlSystem>
<FCSComponent type="FCSRotationDamper">
<YawController P="2" D="0"/>
<PitchController P="2.0" D="0"/>
<RollController P="2" D="0.2"/>
</FCSComponent>
</ControlSystem>
More info about the PID controler concept
If multiple components are defined in the configuration, they are connected to each other in a cascade, i.e. each stage receives its inputs from the previous stage. Only the first stage receives its inputs directly from the pilot. A disabled stage passes its inputs to the next stage without any change. By enabling/disabling the stages, different automatic control system configurations can be obtained. If all stages are disabled, pilot inputs directly control the actuators.
RTD::FCSRotationDamper
This control system component is used to dampen the rotational motion of the helicopter in all three axes. It can be used for both airplane and helicopters. FCSRotationDamper contains, for each rotational degree of freedom, a PD controller.
<FCSComponent type="FCSRotationDamper">
<YawController P D/>
<PitchController P D/>
<RollController P D/>
</FCSComponent>
YawController
Configures the PD controller that damps yawing motion.
- P: Proportional coefficient of the controller.
- D: Derivative coefficient of the controller.
PitchController
Configures the PD controller that damps pitching motion.
- P: Proportional coefficient of the controller.
- D: Derivative coefficient of the controller.
RollController
Configures the PD controller that damps rolling motion.
- P: Proportional coefficient of the controller.
- D: Derivative coefficient of the controller.
RotorLibFDM::FCSHelicopterAutoTrim
This control system component is used to trim the helicopter automatically and hence remove the coupling between controls (i.e. collective / pedal coupling). It translates pilot inputs to requested heading, pitch and roll rates or to requested side slip and controls the actuators to achieve the desired state. The final result is a simpler flight.
FCSHelicopterAutoTrim is suitable for simulators where simple input devices, such as a joystick, is used. In case real helicopter input devices with trim lock controls are used, FCSHelicopterAutoTrim should not be used.
<FSComponent type="FCSHelicopterAutoTrim">
<YawRateAndSideslipController printDebugInfo>
<YawRatePID P I D offset integralMin integralMax />
<SideslipPID P I D offset integralMin integralMax />
<Transition speedLow speedHigh />
<Maximums maxYawRate maxSideslip />
<InputMapping nonlinearity />
</YawRateAndSideslipController>
<PitchRateController printDebugInfo >
<PID P I D offset integralMin integralMax />
<MaxPitchRate maxPitchRate />
</PitchRateController>
<RollRateController printDebugInfo >
<PID P I D offset integralMin integralMax />
<MaxRollRate maxRollRate />
</RollRateController>
<FSComponent type="FCSHelicopterAutoTrim">
YawRateAndSideslipController
This controller controls the pedals to reach and maintain a certain yaw rate or side slip. Yaw rate control mode is active at low speeds, whereas side slip control mode is activated at high speeds. The mode change occurs smoothly within a user defined speed range (see Transition below). Within this transition region, both yaw rate and side slip control modes are active but their contribution to the final output varies depending on speed.
printDebugInfo
A boolean parameter (possible values "true" and "false" ) to enable/disable debug output to the console from the controller. This is useful for the parametrization of the controller.
- YawratePID: Parameters of the PID controller that is used to control yaw rate. Error input to this PID is desired yaw rate - current yaw rate. Desired yaw rate is determined by the pedal input, i.e. pilot's pedal input is translated to a desired yaw rate by the controller.
- P: Proportional coefficient of the controller.
- I: Integral coefficient of the controller.
- D: Derivative coefficient of the controller.
- offset: "Zero point" of the controller. When error, error derivative and error sum is zero resulting value will be offset.
- IntegralMin and integralMax: Minimum/Maximum value the error sum can reach. If the sum of errors go below/above this value it is clamped to this value.
- SideslipPID: Parameters of the PID controller that is used to control side slip. Error input to this PID is desired side slip - current side slip. Desired side slip is determined by the pedal input, i.e. pilot's pedal input is translated to a desired side slip by the controller.
- P: Proportional coefficient of the controller.
- I: Integral coefficient of the controller.
- D: Derivative coefficient of the controller.
- offset: "Zero point" of the controller. When error, error derivative and error sum is zero resulting value will be offset.
- IntegralMin and integralMax: Minimum/Maximum value the error sum can reach. If the sum of errors go below/above this value it is clamped to this value.
- Transition: YawRateAndSideslipController is designed so that it interprets the pilot pedal input as desired yaw rate at low speeds and as desired side slip at high speeds. A transition region based on speed can be defined to enable a smooth transition between these modes.
- speedLow and speedHigh : Below speedLow, the pedal input will be interpreted as desired yaw rate and after speedHigh as desired side slip. Between these two speeds, the outputs of the Yaw Rate and Side slip subcontrollers will be linearly mixed.
- Maximums
- maxYawRate: Maximum yaw rate that can be requested from the controller. This parameter is in deg/s and must be positive always.
- maxSideslip: Maximum side slip angle that can be requested from the controller. This parameter is in degrees and must be positive always.
- InputMapping
- nonlinearity : In some cases, it might be better to pass the pilot input to the control system non-linearly. For example, in a desktop simulator, where the input device is a common joystick, we might want to have a better precision at the zero point. We can define an exponential relationship between pilot's input and the control system input using nonlinearity parameter. The pedal input that is given to the control system is computed as follows: pedal input to controller = (|pilot pedal input| ^ nonlinearity) * sign(pilot pedal input).
PitchRateController, RollRateController =
Controllers for pitch and roll rates.
- PID: Parameters of the PID controller that is used to regulate the rotational motion.
- P: Proportional coefficient of the controller.
- I: Integral coefficient of the controller.
- D: Derivative coefficient of the controller.
- offset: "Zero point" of the controller. When error, error derivative and error sum is zero resulting value will be offset.
- IntegralMin and integralMax: Minimum/Maximum value the error sum can reach. If the sum of errors go below/above this value it is clamped to this value.
- MaxPitchRate and MaxRollRate: These are maximum angular speeds the controllers are trying to reach. E.g. if control stick is pulled 100% right, RollRateController will try to reach a roll rate of maxRollRate. The values are in deg/sec.
- InputMapping
- nonlinearity : In some cases, it might be better to pass the pilot input to the control system non-linearly. For example, in a desktop simulator, where the input device is a common joystick, we might want to have a better precision at the zero point. We can define an exponential relationship between pilot's input and the control system input using nonlinearity parameter. The actual input that is given to the control system is computed as follows: input to controller = (|pilot input| ^ nonlinearity) * sign(pilot input).
Ground contacts
Interaction with terrain is simulated by ground contacts, classes that are derived from RTD::FGGroundContactBase. Highest fidelity ground contact implementation is RTD::FGGroundContact200 class in the current version. Initially gears are extended.
Ground contacts are defined in <GroundContacts> section of the configuration file. Each new ground contact has to be defined in its own section with name <GroundContact>. Also the type of the ground contact has to be declared here using the type attribute. In <GroundContacts> section <GeneralConfiguration> subsection is used to define some parameters that are common to all ground contacts.
<GroundContacts>
<GeneralConfiguration
gearExtensionTime gearDragCoefficient
gearReferenceArea maxSteerableGearDeflection
steerableGearSpeedCorrectionFactor/>
<GroundContact type>
-> Parameters Related to chosen ground contact model <-
</GroundContact>
</GroundContacts>
GeneralConfiguration
- gearExtensionTime: Time needed to extend/retract landing gears in seconds.
- gearDragCoefficient: Coefficient of drag for landing gears.
- gearReferenceArea: Reference area of the landing gears to be used in air drag computation.
- maxSteerableGearDeflection: Maximum deflection (in degrees) of the steerable gears.
- steerableGearSpeedCorrectionFactor: As the speed of the aircraft increases, deflections of steerable gears are automatically reduced to keep the aircraft controllable. This parameter defines the strength of this correction.
GroundContact
A multitude of <GroundContact> </GroundContact> sections can be defined. The type parameter defines which ground contact model (E.g. FGGroundContact200) has to be used. Inside the opening and closing tags, configuration parameters of the chosen model has to be provided.
FGGroundContact200 configuration
FGGroundContact200 implements a multibody dynamics based ground contact model. It supports inclined and moving surfaces (e.g. for ship deck landing).
<GroundContact type="FGGroundContact200">
<Features isBrakable isRetractable isSteerable />
<Suspension>
<MountStation x y z/>
<SliderAxis x y z />
<SuspensionLength length />
<SpringParameters springConstant
damperConstant
maxCompression/>
</Suspension>
<Wheel mass radius>
<RollAxis x y z />
<Friction slidingFriction resistanceTorqueNoBrake
resistanceTorqueFullBrake />
</Wheel>
<SteeringController maxTorque maxRotSpeed
controllerGain inverseRotation
keepCenter />
<Damage thresholdLoad />
</GroundContact>
Features
General features of the ground contact.
- isBrakable: Is the ground contact a brakable landing gear? (true or false)
- isRetractable: Is the ground contact a retractable landing gear? (true or false)
- isSteerable: Is the ground contact a steerable landing gear? (true or false)
Suspension
Parameters of the suspension.
- MountStation: Position at which the landing gear is mounted onto the aircraft body. Relative to center of gravity and in meters.
- SliderAxis: This is a unit direction vector which determines along which direction suspension slider can move. It is defined relative to aircraft body coordinates in RTDDynamics coordinate system convention.
- SuspensionLength: Length of the suspension, i.e. the distance from mount station to middle point of wheel when suspensions are not compressed or decompressed. In meters.
- SpringParameters
- springConstant: Spring constant of the suspension spring. In N/m.
- damperConstant: Damper constant of the suspension spring. In N*sec/meter.
- maxCompression: Maximum amount the suspension spring can be compressed. This value should be less than or equal to suspension length. In meters.
Wheel
Parameters of the wheel.
- mass: Mass in Kg.
- radius: Radius of the wheel in meters.
- rotationalInertia: Rotational inertia of the wheel in Kg*m^2.
- RollAxis: A direction vector that defines the axis of wheel rotation. It is defined relative to aircraft body coordinates.
- Friction
- slidingFriction: Coefficient of friction between the tire and the ground.
- resistanceTorqueNoBrake and resistanceTorqueFullBrake: An effective resistance torque from linear interpolation of resistanceTorqueNoBrake and resistanceTorqueFullBrake depending on the amount of applied wheel brake is applied to the wheel continuously to simulate rolling friction. The resistance torque acts in a direction that opposes the current rotation of the wheel. In N*m.
SteeringController
- maxTorque: The steering controller rotates the wheel left or right depending on the pilot's input for steering on the ground. This parameter defines how much torque can be applied to the wheel for this purpose. This parameter is in N*m.
- maxRotSpeed: This parameter defines how fast the wheel can rotate around the vertical axis. In Deg/sec.
- controllerGain: The torque applied to the wheel to rotate it is proportional to the difference of pilot's desired wheel direction and current direction multiplied by \e m_steeringControllerGain (the result is clamped at \e m_steeringMaxTorque ). This parameter is unitless.
- inverseRotation: If this parameter is set to true, the wheel will rotate in the opposite direction of the pilot input (if pilot input is to the right wheel will rotate to the left etc. ). This is necessary if the steering wheel is at the back instead of front.
- keepCenter: If this parameter is set to true, the wheel will not be affected by the pilot's control input but instead will try to keep the wheel in center always. This is useful to model free rotating wheels (a wheel that can rotate around vertical axis but is not actively controlled by actuators ).
Damage
- thresholdLoad: During landing the forces acting on the wheel are transferred to the fuselage. Beyond a certain threshold the transferred forces result in damage in the aircraft. The load defined in thresholdLoad (in N) is the threshold used for this purpose.